Giải thuật và lập trình: §9. Tìm kiếm (SEARCHING)
BÀI TOÁN TÌM KIẾM
Cùng với sắp xếp, tìm kiếm là một đòi hỏi rất thường xuyên trong các ứng dụng tin học. Bài toán tìm kiếm có thể phát biểu như sau:
Cho một dãy gồm n bản ghi r1, r2, …, rn. Mỗi bản ghi ri (1 ≤ i ≤ n) tương ứng với một khoá ki.
Hãy tìm bản ghi có giá trị khoá bằng X cho trước.
X được gọi là khoá tìm kiếm hay đối trị tìm kiếm (argument).
Công việc tìm kiếm sẽ hoàn thành nếu như có một trong hai tình huống sau xảy ra:
- Tìm được bản ghi có khoá tương ứng bằng X, lúc đó phép tìm kiếm thành công (successful).
- Không tìm được bản ghi nào có khoá tìm kiếm bằng X cả, phép tìm kiếm thất bại (unsuccessful).
Tương tự như sắp xếp, ta coi khoá của một bản ghi là đại diện cho bản ghi đó. Và trong một số thuật toán sẽ trình bày dưới đây, ta coi kiểu dữ liệu cho mỗi khoá cũng có tên gọi là TKey.
const
n = …; {Số khoá trong dãy khoá, có thể khai dưới dạng biến số nguyên để tuỳ biến hơn}
type
TKey = …; {Kiểu dữ liệu một khoá}
TArray = array[1..n] of TKey;
var
k: TArray; {Dãy khoá}
TÌM KIẾM TUẦN TỰ (SEQUENTIALSEARCH)
Tìm kiếm tuần tự là một kỹ thuật tìm kiếm đơn giản. Nội dung của nó như sau: Bắt đầu từ bản ghi đầu tiên, lần lượt so sánh khoá tìm kiếm với khoá tương ứng của các bản ghi trong danh sách, cho tới khi tìm thấy bản ghi mong muốn hoặc đã duyệt hết danh sách mà chưa thấy
{Tìm kiếm tuần tự trên dãy khoá k1, k2, …, kn; hàm này thử tìm xem trong dãy có khoá nào = X không, nếu thấy nó trả về chỉ số của khoá ấy, nếu không thấy nó trả về 0. Có sử dụng một khoá phụ kn+1 được gán giá trị = X}
function SequentialSearch(X: TKey): Integer;
var
i: Integer;
begin
i := 1;
while (i <= n) and (ki ≠ X) do i := i + 1;
if i = n + 1 then SequentialSearch := 0
else SequentialSearch := i;
end;
Dễ thấy rằng độ phức tạp của thuật toán tìm kiếm tuần tự trong trường hợp tốt nhất là O(1), trong trường hợp xấu nhất là O(n) và trong trường hợp trung bình cũng là O(n).
TÌM KIẾM NHỊ PHÂN (BINARYSEARCH)
Phép tìm kiếm nhị phân có thể áp dụng trên dãy khoá đã có thứ tự: k1 ≤ k2 ≤ … ≤ kn.
Giả sử ta cần tìm trong đoạn kinf, kinf+1, …, ksup với khoá tìm kiếm là X, trước hết ta xét khoá nằm giữa dãy kmedian với median = (inf + sup) div 2;
Nếu kmedian < X thì có nghĩa là đoạn từ kinf tới kmedian chỉ chứa toàn khoá < X, ta tiến hành tìm kiếm tiếp với đoạn từ kmedian + 1 tới ksup.
Nếu kmedian > X thì có nghĩa là đoạn từ kmedian tới ksup chỉ chứa toàn khoá > X, ta tiến hành tìm kiếm tiếp với đoạn từ kinf tới kmedian - 1.
Nếu kmedian = X thì việc tìm kiếm thành công (kết thúc quá trình tìm kiếm).
Quá trình tìm kiếm sẽ thất bại nếu đến một bước nào đó, đoạn tìm kiếm là rỗng (inf > sup).
{Tìm kiếm nhị phân trên dãy khoá k1 ≤ k2 ≤ … ≤ kn; hàm này thử tìm xem trong dãy có khoá nào = X không, nếu thấy nó trả về chỉ số của khoá ấy, nếu không thấy nó trả về 0}
function BinarySearch(X: TKey): Integer;
var
inf, sup, median: Integer;
begin
inf := 1;
sup := n;
while inf ≤ sup do
begin
median := (inf + sup) div 2;
if kmedian = X then
begin
BinarySearch := median;
Exit;
end;
if kmedian < X then inf := median + 1
else sup := median - 1;
end;
BinarySearch := 0;
end;
Người ta đã chứng minh được độ phức tạp tính toán của thuật toán tìm kiếm nhị phân trong trường hợp tốt nhất là O(1), trong trường hợp xấu nhất là O(log2n) và trong trường hợp trung bình cũng là O(log2n). Tuy nhiên, ta không nên quên rằng trước khi sử dụng tìm kiếm nhị phân, dãy khoá phải được sắp xếp rồi, tức là thời gian chi phí cho việc sắp xếp cũng phải tính đến. Nếu dãy khoá luôn luôn biến động bởi phép bổ sung hay loại bớt đi thì lúc đó chi phí cho sắp xếp lại nổi lên rất rõ làm bộc lộ nhược điểm của phương pháp này.
CÂY NHỊ PHÂN TÌM KIẾM (BINARY SEARCH TREE - BST)
Cho n khoá k1, k2, …, kn, trên các khoá có quan hệ thứ tự toàn phần. Cây nhị phân tìm kiếm ứng với dãy khoá đó là một cây nhị phân mà mỗi nút chứa giá trị một khoá trong n khoá đã cho, hai giá trị chứa trong hai nút bất kỳ là khác nhau. Đối với mọi nút trên cây, tính chất sau luôn được thoả mãn:
- Mọi khoá nằm trong cây con trái của nút đó đều nhỏ hơn khoá ứng với nút đó.
- Mọi khoá nằm trong cây con phải của nút đó đều lớn hơn khoá ứng với nút đó.

Hình 1: Cây nhị phân tìm kiếm
Thuật toán tìm kiếm trên cây có thể mô tả chung như sau:
Trước hết, khoá tìm kiếm X được so sánh với khoá ở gốc cây, và 4 tình huống có thể xảy ra:
- Không có gốc (cây rỗng): X không có trên cây, phép tìm kiếm thất bại.
- X trùng với khoá ở gốc: Phép tìm kiếm thành công.
- X nhỏ hơn khoá ở gốc, phép tìm kiếm được tiếp tục trong cây con trái của gốc với cách làm tương tự.
- X lớn hơn khoá ở gốc, phép tìm kiếm được tiếp tục trong cây con phải của gốc với cách làm tương tự.
Giả sử cấu trúc một nút của cây được mô tả như sau:
type
PNode = ^TNode; {Con trỏ chứa liên kết tới một nút}
TNode = record {Cấu trúc nút}
Info: TKey; {Trường chứa khoá}
Left, Right: PNode; {con trỏ tới nút con trái và phải, trỏ tới nil nếu không có nút con trái (phải)}
end;
Gốc của cây được lưu trong con trỏ Root. Cây rỗng thì Root = nil
Thuật toán tìm kiếm trên cây nhị phân tìm kiếm có thể viết như sau:
{Hàm tìm kiếm trên BST, nó trả về nút chứa khoá tìm kiếm X nếu tìm thấy, trả về nil nếu không tìm thấy}
function BSTSearch(X: TKey): PNode;
var
p: PNode;
begin
p := Root; {Bắt đầu với nút gốc}
while p ≠ nil do
if X = p^.Info then Break;
else
if X < p^.Info then p := p^.Left
else p := p^.Right;
BSTSearch := p;
end;
Thuật toán dựng cây nhị phân tìm kiếm từ dãy khoá k1, k2, …, kn cũng được làm gần giống quá trình tìm kiếm. Ta chèn lần lượt các khoá vào cây, trước khi chèn, ta tìm xem khoá đó đã có trong cây hay chưa, nếu đã có rồi thì bỏ qua, nếu nó chưa có thì ta thêm nút mới chứa khoá cần chèn và nối nút đó vào cây nhị phân tìm kiếm.
{Thủ tục chèn khoá X vào BST}
procedure BSTInsert(X);
var
p, q: PNode;
begin
q := nil;
p := Root; {Bắt đầu với p = nút gốc; q là con trỏ chạy đuổi theo sau}
while p ≠ nil do
begin
q := p;
if X = p^.Info then Break;
else {X ≠ p^.Info thì cho p chạy sang nút con, q^ luôn giữ vai trò là cha của p^}
if X < p^.Info then p := p^.Left
else p := p^.Right;
end;
if p = nil then {Khoá X chưa có trong BST}
begin
New(p); {Tạo nút mới}
p^.Info := X; {Đưa giá trị X vào nút mới tạo ra}
p^.Left := nil;
p^.Right := nil; {Nút mới khi chèn vào BST sẽ trở thành nút lá}
if Root = nil then Root := NewNode {BST đang rỗng, đặt Root là nút mới tạo}
else {Móc NewNode^ vào nút cha q^}
if X < q^.Info then q^.Left := NewNode
else q^.Right := NewNode;
end;
end;
Phép loại bỏ trên cây nhị phân tìm kiếm không đơn giản như phép bổ sung hay phép tìm kiếm.
Muốn xoá một giá trị trong cây nhị phân tìm kiếm (Tức là dựng lại cây mới chứa tất cả những giá trị còn lại), trước hết ta tìm xem giá trị cần xoá nằm ở nút D nào, có ba khả năng xảy ra:
- Nút D là nút lá, trường hợp này ta chỉ việc đem mối nối cũ trỏ tới nút D (từ nút cha của D) thay bởi nil, và giải phóng bộ nhớ cấp cho nút D (Hình 2).
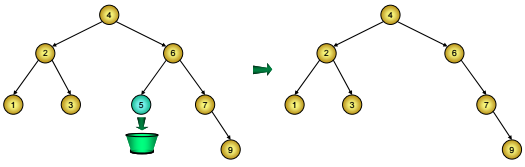
Hình 2: Xóa nút lá ở cây BST
- Nút D chỉ có một nhánh con, khi đó ta đem nút gốc của nhánh con đó thế vào chỗ nút D, tức là chỉnh lại mối nối: Từ nút cha của nút D không nối tới nút D nữa mà nối tới nhánh con duy nhất của nút D. Cuối cùng, ta giải phóng bộ nhớ đã cấp cho nút D (Hình 3).
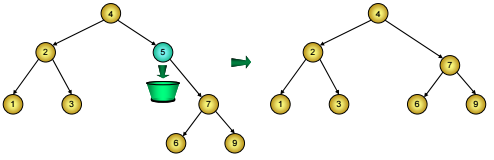
Hình 3: Xóa nút chỉ có một nhánh con trên cây BST
- Nút D có cả hai nhánh con trái và phải, khi đó có hai cách làm đều hợp lý cả:
o Hoặc tìm nút chứa khoá lớn nhất trong cây con trái, đưa giá trị chứa trong đó sang nút D, rồi xoá nút này. Do tính chất của cây BST, nút chứa khoá lớn nhất trong cây con trái chính là nút cực phải của cây con trái nên nó không thể có hai con được, việc xoá đưa về hai trường hợp trên (Hình 4)
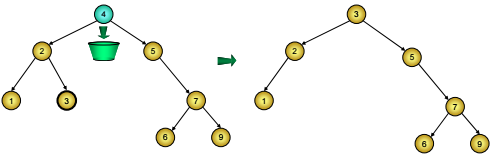
Hình 4: Xóa nút có cả hai nhánh con trên cây BST thay bằng nút cực phải của cây con trái
o Hoặc tìm nút chứa khoá nhỏ nhất trong cây con phải, đưa giá trị chứa trong đó sang nút D, rồi xoá nút này. Do tính chất của cây BST, nút chứa khoá nhỏ nhất trong cây con phải chính là nút cực trái của cây con phải nên nó không thể có hai con được, việc xoá đưa về hai trường hợp trên.
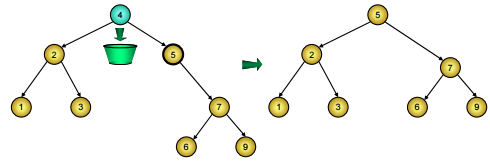
Hình 5: Xóa nút có cả hai nhánh con trên cây BST thay bằng nút cực trái của cây con phải
{Thủ tục xoá khoá X khỏi BST}
procedure BSTDelete(X: TKey);
var
p, q, Node, Child: PNode;
begin
p := Root;
q := nil; {Về sau, khi p trỏ sang nút khác, ta luôn giữ cho q^ luôn là cha của p^}
while p ≠ nil do {Tìm xem trong cây có khoá X không?}
begin
if p^.Info = X then Break; {Tìm thấy}
q := p;
if X < p^.Info then p := p^.Left
else p := p^.Right;
end;
if p = nil then Exit; {X không tồn tại trong BST nên không xoá được}
if (p^.Left ≠ nil) and (p^.Right ≠ nil) then {p^ có cả con trái và con phải}
begin
Node := p; {Giữ lại nút chứa khoá X}
q := p; p := p^.Left; {Chuyển sang nhánh con trái để tìm nút cực phải}
while p^.Right ≠ nil do
begin
q := p;
p := p^.Right;
end;
Node^.Info := p^.Info; {Chuyển giá trị từ nút cực phải trong nhánh con trái lên Node^}
end;
{Nút bị xoá giờ đây là nút p^, nó chỉ có nhiều nhất một con}
{Nếu p^ có một nút con thì đem Child trỏ tới nút con đó, nếu không có thì Child = nil }
if p^.Left ≠ nil then Child := p^.Left
else Child := p^.Right;
if p = Root then Root := Child; {Nút p^ bị xoá là gốc cây}
else {Nút bị xoá p^ không phải gốc cây thì lấy mối nối từ cha của nó là q^ nối thẳng tới Child}
if q^.Left = p then q^.Left := Child
else q^.Right := Child;
Dispose(p);
end;
Trường hợp trung bình, thì các thao tác tìm kiếm, chèn, xoá trên BST có độ phức tạp là O(log2n). Còn trong trường hợp xấu nhất, cây nhị phân tìm kiếm bị suy biến thì các thao tác đó đều có độ phức tạp là O(n), với n là số nút trên cây BST.
Nếu ta mở rộng hơn khái niệm cây nhị phân tìm kiếm như sau: Giá trị lưu trong một nút lớn hơn hoặc bằng các giá trị lưu trong cây con trái và nhỏ hơn các giá trị lưu trong cây con phải. Thì chỉ cần sửa đổi thủ tục BSTInsert một chút, khi chèn lần lượt vào cây n giá trị, cây BST sẽ có n nút (có thể có hai nút chứa cùng một giá trị). Khi đó nếu ta duyệt các nút của cây theo kiểu trung thứ tự (inorder traversal), ta sẽ liệt kê được các giá trị lưu trong cây theo thứ tự tăng dần. Phương pháp sắp xếp này người ta gọi là Tree Sort. Độ phức tạp tính toán trung bình của Tree Sort là O(nlog2n).
Phép tìm kiếm trên cây BST sẽ kém hiệu quả nếu như cây bị suy biến, người ta có nhiều cách xoay xở để tránh trường hợp này. Đó là phép quay cây để dựng cây nhị phân cân đối AVL, hay kỹ thuật dựng cây nhị phân tìm kiếm tối ưu. Những kỹ thuật này ta có thể tham khảo trong các tài liệu khác về cấu trúc dữ liệu và giải thuật.
PHÉP BĂM (HASH)
Tư tưởng của phép băm là dựa vào giá trị các khoá k1, k2, …, kn, chia các khoá đó ra thành các nhóm. Những khoá thuộc cùng một nhóm có một đặc điểm chung và đặc điểm này không có trong các nhóm khác. Khi có một khoá tìm kiếm X, trước hết ta xác định xem nếu X thuộc vào dãy khoá đã cho thì nó phải thuộc nhóm nào và tiến hành tìm kiếm trên nhóm đó.
Một ví dụ là trong cuốn từ điển, các bạn sinh viên thường dán vào 26 mảnh giấy nhỏ vào các trang để đánh dấu trang nào là trang khởi đầu của một đoạn chứa các từ có cùng chữ cái đầu. Để khi tra từ chỉ cần tìm trong các trang chứa những từ có cùng chữ cái đầu với từ cần tìm.

Một ví dụ khác là trên dãy các khoá số tự nhiên, ta có thể chia nó là làm m nhóm, mỗi nhóm gồm các khoá đồng dư theo mô-đun m.
Có nhiều cách cài đặt phép băm:
- Cách thứ nhất là chia dãy khoá làm các đoạn, mỗi đoạn chứa những khoá thuộc cùng một nhóm và ghi nhận lại vị trí các đoạn đó. Để khi có khoá tìm kiếm, có thể xác định được ngay cần phải tìm khoá đó trong đoạn nào.
- Cách thứ hai là chia dãy khoá làm m nhóm, Mỗi nhóm là một danh sách nối đơn chứa các giá trị khoá và ghi nhận lại chốt của mỗi danh sách nối đơn. Với một khoá tìm kiếm, ta xác định được phải tìm khoá đó trong danh sách nối đơn nào và tiến hành tìm kiếm tuần tự trên danh sách nối đơn đó. Với cách lưu trữ này, việc bổ sung cũng như loại bỏ một giá trị khỏi tập hợp khoá dễ dàng hơn rất nhiều phương pháp trên.
- Cách thứ ba là nếu chia dãy khoá làm m nhóm, mỗi nhóm được lưu trữ dưới dạng cây nhị phân tìm kiếm và ghi nhận lại gốc của các cây nhị phân tìm kiếm đó, phương pháp này có thể nói là tốt hơn hai phương pháp trên, tuy nhiên dãy khoá phải có quan hệ thứ tự toàn phần thì mới làm được.
KHOÁ SỐ VỚI BÀI TOÁN TÌM KIẾM
Mọi dữ liệu lưu trữ trong máy tính đều được số hoá, tức là đều được lưu trữ bằng các đơn vị Bit, Byte, Word v.v… Điều đó có nghĩa là một giá trị khoá bất kỳ, ta hoàn toàn có thể biết được nó được mã hoá bằng con số như thế nào. Và một điều chắc chắn là hai khoá khác nhau sẽ được lưu trữ bằng hai số khác nhau.
Đối với bài toán sắp xếp, ta không thể đưa việc sắp xếp một dãy khoá bất kỳ về việc sắp xếp trên một dãy khoá số là mã của các khoá. Bởi quan hệ thứ tự trên các con số đó có thể khác với thứ tự cần sắp của các khoá.
Nhưng đối với bài toán tìm kiếm thì khác, với một khoá tìm kiếm, Câu trả lời hoặc là "Không tìm thấy" hoặc là "Có tìm thấy và ở chỗ …" nên ta hoàn toàn có thể thay các khoá bằng các mã số của nó mà không bị sai lầm, chỉ lưu ý một điều là: hai khoá khác nhau phải mã hoá thành hai số khác nhau mà thôi.
Nói như vậy có nghĩa là việc nghiên cứu những thuật toán tìm kiếm trên các dãy khoá số rất quan trọng, và dưới đây ta sẽ trình bày một số phương pháp đó.
CÂY TÌM KIẾM SỐ HỌC (DIGITAL SEARCH TREE -DST)
Xét dãy khoá k1, k2, …, kn là các số tự nhiên, mỗi giá trị khoá khi đổi ra hệ nhị phân có z chữ số nhị phân (bit), các bit này được đánh số từ 0 (là hàng đơn vị) tới z - 1 từ phải sang trái.
Ví dụ:

Hình 6: Đánh số các bit
Cây tìm kiếm số học chứa các giá trị khoá này có thể mô tả như sau: Trước hết, nó là một cây nhị phân mà mỗi nút chứa một giá trị khoá. Nút gốc có tối đa hai cây con, ngoài giá trị khoá chứa ở nút gốc, tất cả những giá trị khoá có bit cao nhất là 0 nằm trong cây con trái, còn tất cả những giá trị khoá có bit cao nhất là 1 nằm ở cây con phải. Đối với hai nút con của nút gốc, vấn đề tương tự đối với bit z - 2 (bit đứng thứ nhì từ trái sang).
So sánh cây tìm kiếm số học với cây nhị phân tìm kiếm, chúng chỉ khác nhau về cách chia hai cây con trái/phải. Đối với cây nhị phân tìm kiếm, việc chia này được thực hiện bằng cách so sánh với khoá nằm ở nút gốc, còn đối với cây tìm kiếm số học, nếu nút gốc có mức là d thì việc chia cây con được thực hiện theo bit thứ d tính từ trái sang (bit z - d) của mỗi khoá.
Ta nhận thấy rằng những khoá bắt đầu bằng bit 0 chắc chắn nhỏ hơn những khoá bắt đầu bằng bit 1, đó là điểm tương đồng giữa cây nhị phân tìm kiếm và cây tìm kiếm số học: Với mỗi nút nhánh: Mọi giá trị chứa trong cây con trái đều nhỏ hơn giá trị chứa trong cây con phải (Hình 7).

Hình 7: Cây tìm kiếm số học
Giả sử cấu trúc một nút của cây được mô tả như sau:
type
PNode = ^TNode; {Con trỏ chứa liên kết tới một nút}
TNode = record {Cấu trúc nút}
Info: TKey; {Trường chứa khoá}
Left, Right: PNode; {con trỏ tới nút con trái và phải, trỏ tới nil nếu không có nút con trái (phải)}
end;
Gốc của cây được lưu trong con trỏ Root. Ban đầu nút Root = nil (cây rỗng)
Với khoá tìm kiếm X, việc tìm kiếm trên cây tìm kiếm số học có thể mô tả như sau: Ban đầu đứng ở nút gốc, xét lần lượt các bit của X từ trái sang phải (từ bit z - 1 tới bit 0), hễ gặp bit bằng 0 thì rẽ sang nút con trái, nếu gặp bit bằng 1 thì rẽ sang nút con phải. Quá trình cứ tiếp tục như vậy cho tới khi gặp một trong hai tình huống sau:
- Đi tới một nút rỗng (do rẽ theo một liên kết nil), quá trình tìm kiếm thất bại do khoá X không có trong cây.
- Đi tới một nút mang giá trị đúng bằng X, quá trình tìm kiếm thành công
{Hàm tìm kiếm trên cây tìm kiếm số học, nó trả về nút chứa khoá tìm kiếm X nếu tìm thấy, trả về nil nếu không tìm thấy. z là độ dài dãy bit biểu diễn một khoá}
function DSTSearch(X: TKey): PNode;
var
b: Integer;
p: PNode;
begin
b := z;
p := Root; {Bắt đầu với nút gốc}
while (p ≠ nil) and (p^.Info ≠ X) do {Chưa gặp phải một trong 2 tình huống trên}
begin
b := b - 1; {Xét bit b của X}
if <Bit b của X là 0> then p := p^.Left {Gặp 0 rẽ trái}
else p := p^.Right; {Gặp 1 rẽ phải}
end;
DSTSearch := p;
end;
Thuật toán dựng cây tìm kiếm số học từ dãy khoá k1, k2, …, kn cũng được làm gần giống quá trình tìm kiếm. Ta chèn lần lượt các khoá vào cây, trước khi chèn, ta tìm xem khoá đó đã có trong cây hay chưa, nếu đã có rồi thì bỏ qua, nếu nó chưa có thì ta thêm nút mới chứa khoá cần chèn và nối nút đó vào cây tìm kiếm số học tại mối nối rỗng vừa rẽ sang khiến quá trình tìm kiếm thất bại
{Thủ tục chèn khoá X vào cây tìm kiếm số học}
procedure DSTInsert(X: TKey);
var
b: Integer;
p, q: PNode;
begin
b := z;
p := Root;
while (p ≠ nil) and (p^.Info ≠ X) do
begin
b := b - 1; {Xét bit b của X}
q := p; {Khi p chạy xuống nút con thì q^ luôn giữ vai trò là nút cha của p^}
if <Bit b của X là 0> then p := p^.Left {Gặp 0 rẽ trái}
else p := p^.Right; {Gặp 1 rẽ phải}
end;
if p = nil then {Giá trị X chưa có trong cây}
begin
New(p); {Tạo ra một nút mới p^}
p^.Info := X; {Nút mới tạo ra sẽ chứa khoá X}
p^.Left := nil; p^.Right := nil; {Nút mới đó sẽ trở thành một lá của cây}
if Root = nil then Root := p {Cây đang là rỗng thì nút mới thêm trở thành gốc}
else {Không thì móc p^ vào mối nối vừa rẽ sang từ q^}
if <Bit b của X là 0> then q^.Left := p
else q^.Right := p;
end;
end;
Muốn xoá bỏ một giá trị khỏi cây tìm kiếm số học, trước hết ta xác định nút chứa giá trị cần xoá là nút D nào, sau đó tìm trong nhánh cây gốc D ra một nút lá bất kỳ, chuyển giá trị chứa trong nút lá đó sang nút D rồi xoá nút lá.
{Thủ tục xoá khoá X khỏi cây tìm kiếm số học}
procedure DSTDelete(X: TKey);
var
b: Integer;
p, q, Node: PNode;
begin
{Trước hết, tìm kiếm giá trị X xem nó nằm ở nút nào}
b := z;
p := Root;
while (p ≠ nil) and (p^.Info ≠ X) do
begin
b := b - 1;
q := p; {Mỗi lần p chuyển sang nút con, ta luôn đảm bảo cho q^ là nút cha của p^}
if <Bit b của X là 0> then p := p^.Left
else p := p^.Right;
end;
if p = nil then Exit; {X không tồn tại trong cây thì không xoá được}
Node := p; {Giữ lại nút chứa khoá cần xoá}
while (p^.Left ≠ nil) or (p^.Right ≠ nil) do {chừng nào p^ chưa phải là lá}
begin
q := p; {q chạy đuổi theo p, còn p chuyển xuống một trong 2 nhánh con}
if p^.Left ≠ nil then p := p^.Left
else p := p^.Right;
end;
Node^.Info := p^.Info; {Chuyển giá trị từ nút lá p^ sang nút Node^}
if Root = p then Root := nil {Cây chỉ gồm một nút gốc và bây giờ xoá cả gốc}
else {Cắt mối nối từ q^ tới p^}
if q^.Left = p then q^.Left := nil
else q^.Right := nil;
Dispose(p);
end;
Về mặt trung bình, các thao tác tìm kiếm, chèn, xoá trên cây tìm kiếm số học đều có độ phức tạp là O(log2n) còn trong trường hợp xấu nhất, độ phức tạp của các thao tác đó là O(z), bởi cây tìm kiếm số học có chiều cao không quá z + 1.
CÂY TÌM KIẾM CƠ SỐ (RADIX SEARCH TREE -RST)
Trong cây tìm kiếm số học, cũng như cây nhị phân tìm kiếm, phép tìm kiếm tại mỗi bước phải so sánh giá trị khoá X với giá trị lưu trong một nút của cây. Trong trường hợp các khoá có cấu trúc lớn, việc so sánh này có thể mất nhiều thời gian.
Cây tìm kiếm cơ số là một phương pháp khắc phục nhược điểm đó, nội dung của nó có thể tóm tắt như sau:
Trong cây tìm kiếm cơ số là một cây nhị phân, chỉ có nút lá chứa giá trị khoá, còn giá trị chứa trong các nút nhánh là vô nghĩa. Các nút lá của cây tìm kiếm cơ số đều nằm ở mức z + 1.
Đối với nút gốc của cây tìm kiếm cơ số, nó có tối đa hai nhánh con, mọi khoá chứa trong nút lá của nhánh con trái đều có bit cao nhất là 0, mọi khoá chứa trong nút lá của nhánh con phải đều có bit cao nhất là 1.
Đối với hai nhánh con của nút gốc, vấn đề tương tự với bit thứ z - 2, ví dụ với nhánh con trái của nút gốc, nó lại có tối đa hai nhánh con, mọi khoá chứa trong nút lá của nhánh con trái đều có bit thứ z - 2 là 0 (chúng bắt đầu bằng hai bit 00), mọi khoá chứa trong nút lá của nhánh con phải đều có bit thứ z - 2 là 1 (chúng bắt đầu bằng hai bit 01)…
Tổng quát với nút ở mức d, nó có tối đa hai nhánh con, mọi nút lá của nhánh con trái chứa khoá có bit z - d là 0, mọi nút lá của nhánh con phải chứa khoá có bit thứ z - d là 1 (Hình 8).

Hình 8: Cây tìm kiếm cơ số
Khác với cây nhị phân tìm kiếm hay cây tìm kiếm số học. Cây tìm kiếm cơ số được khởi tạo gồm có một nút gốc, và nút gốc tồn tại trong suốt quá trình sử dụng: nó không bao giờ bị xoá đi cả.
Để tìm kiếm một giá trị X trong cây tìm kiếm cơ số, ban đầu ta đứng ở nút gốc và duyệt dãy bit của X từ trái qua phải (từ bit z - 1 đến bit 0), gặp bit bằng 0 thì rẽ sang nút con trái còn gặp bit bằng 1 thì rẽ sang nút con phải, cứ tiếp tục như vậy cho tới khi một trong hai tình huống sau xảy ra:
- Hoặc đi tới một nút rỗng (do rẽ theo liên kết nil) quá trình tìm kiếm thất bại do X không có trong RST
- Hoặc đã duyệt hết dãy bit của X và đang đứng ở một nút lá, quá trình tìm kiếm thành công vì chắc chắn nút lá đó chứa giá trị đúng bằng X.
{Hàm tìm kiếm trên cây tìm kiếm cơ số, nó trả về nút lá chứa khoá tìm kiếm X nếu tìm thấy, trả về nil nếu không tìm thấy. z là độ dài dãy bit biểu diễn một khoá}
function RSTSearch(X: TKey): PNode;
var
b: Integer;
p: PNode;
begin
b := z; p := Root; {Bắt đầu với nút gốc, đối với RST thì gốc luôn có sẵn}
repeat
b := b - 1; {Xét bit b của X}
if <Bit b của X là 0> then p := p^.Left {Gặp 0 rẽ trái}
else p := p^.Right; {Gặp 1 rẽ phải}
until (p = nil) or (b = 0);
RSTSearch := p;
end;
Thao tác chèn một giá trị X vào RST được thực hiện như sau: Đầu tiên, ta đứng ở gốc và duyệt dãy bit của X từ trái qua phải (từ bit z - 1 về bit 0), cứ gặp 0 thì rẽ trái, gặp 1 thì rẽ phải. Nếu quá trình rẽ theo một liên kết nil (đi tới nút rỗng) thì lập tức tạo ra một nút mới, và nối vào theo liên kết đó để có đường đi tiếp. Sau khi duyệt hết dãy bit của X, ta sẽ dừng lại ở một nút lá của RST, và công việc cuối cùng là đặt giá trị X vào nút lá đó.
Ví dụ:

Hình 9: Với độ dài dãy bit z = 3, cây tìm kiếm cơ số gồm các khoá 2, 4, 5 và sau khi thêm giá trị 7
{Thủ tục chèn khoá X vào cây tìm kiếm cơ số}
procedure RSTInsert(X: TKey);
var
b: Integer;
p, q: PNode;
begin
b := z;
p := Root; {Bắt đầu từ nút gốc, đối với RST thì gốc luôn ¹ nil}
repeat
b := b - 1; {Xét bit b của X}
q := p; {Khi p chạy xuống nút con thì q^ luôn giữ vai trò là nút cha của p^}
if <Bit b của X là 0> then p := p^.Left {Gặp 0 rẽ trái}
else p := p^.Right; {Gặp 1 rẽ phải}
if p = nil then {Không đi được thì đặt thêm nút để đi tiếp}
begin
New(p); {Tạo ra một nút mới và đem p trỏ tới nút đó}
p^.Left := nil;
p^.Right := nil;
if <Bit b của X là 0> then q^.Left := p {Nối p^ vào bên trái q^}
else q^.Right := p; {Nối p^ vào bên phải q^}
end;
until b = 0;
p^.Info := X; {p^ là nút lá để đặt X vào}
end;
Với cây tìm kiếm cơ số, việc xoá một giá trị khoá không phải chỉ là xoá riêng một nút lá mà còn phải xoá toàn bộ nhánh độc đạo đi tới nút đó để tránh lãng phí bộ nhớ (Hình 10).
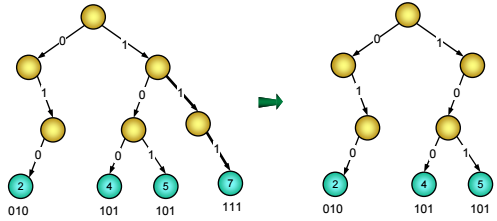
Hình 10: RST chứa các khoá 2, 4, 5, 7 và RST sau khi loại bỏ giá trị 7
Ta lặp lại quá trình tìm kiếm giá trị khoá X, quá trình này sẽ đi từ gốc xuống lá, tại mỗi bước đi, mỗi khi gặp một nút ngã ba (nút có cả con trái và con phải - nút cấp hai), ta ghi nhận lại ngã ba đó và hướng rẽ. Kết thúc quá trình tìm kiếm ta giữ lại được ngã ba đi qua cuối cùng, từ nút đó tới nút lá chứa X là con đường độc đạo (không có chỗ rẽ), ta tiến hành dỡ bỏ tất cả các nút trên đoạn đường độc đạo khỏi cây tìm kiếm cơ số. Để không bị gặp lỗi khi cây suy biến (không có nút cấp 2) ta coi gốc cũng là nút ngã ba.
{Thủ tục xoá khoá X khỏi cây tìm kiếm cơ số}
procedure RSTDelete(X: TKey);
var
b: Integer;
p, q, TurnNode, Child: PNode;
begin
{Trước hết, tìm kiếm giá trị X xem nó nằm ở nút nào}
b := z;
p := Root;
repeat
b := b - 1;
q := p; {Mỗi lần p chuyển sang nút con, ta luôn đảm bảo cho q^ là nút cha của p^}
if <Bit b của X là 0> then p := p^.Left
else p := p^.Right;
if (b = z - 1) or (q^.Left ≠ nil) and (q^.Right ≠ nil) then {q^ là nút ngã ba}
begin
TurnNode := q;
Child := p; {Ghi nhận lại q^ và hướng rẽ}
end;
until (p = nil) or (b = 0);
if p = nil then Exit; {X không tồn tại trong cây thì không xoá được}
{Trước hết, cắt nhánh độc đạo ra khỏi cây}
if TurnNode^.Left = Child then TurnNode^.Left := nil
else TurnNode^.Right := nil
p := Child; {Chuyển sang đoạn đường độc đạo, bắt đầu xoá}
repeat
q := p;
{Lưu ý rằng p^ chỉ có tối đa một nhánh con mà thôi, cho p trỏ sang nhánh con duy nhất nếu có}
if p^.Left ≠ nil then p := p^.Left
else p := p^.Right;
Dispose(q); {Giải phóng bộ nhớ cho nút q^}
until p = nil;
end;
Ta có một nhận xét là: Hình dáng của cây tìm kiếm cơ số không phụ thuộc vào thứ tự chèn các khoá vào mà chỉ phụ thuộc vào giá trị của các khoá chứa trong cây.
Đối với cây tìm kiếm cơ số, độ phức tạp tính toán cho các thao tác tìm kiếm, chèn, xoá trong trường hợp xấu nhất cũng như trung bình đều là O(z). Do không phải so sánh giá trị khoá dọc đường đi, nó nhanh hơn cây tìm kiếm số học nếu như gặp các khoá cấu trúc lớn. Tốc độ như vậy có thể nói là tốt, nhưng vấn đề bộ nhớ khiến ta phải xem xét: Giá trị chứa trong các nút nhánh của cây tìm kiếm cơ số là vô nghĩa dẫn tới sự lãng phí bộ nhớ.
Một giải pháp cho vấn đề này là: Duy trì hai dạng nút trên cây tìm kiếm cơ số: Dạng nút nhánh chỉ chứa các liên kết trái, phải và dạng nút lá chỉ chứa giá trị khoá. Cài đặt cây này trên một số ngôn ngữ định kiểu quá mạnh đôi khi rất khó.
Giải pháp thứ hai là đặc tả một cây tương tự như RST, nhưng sửa đổi một chút: nếu có nút lá chứa giá trị X được nối với cây bằng một nhánh độc đạo thì cắt bỏ nhánh độc đạo đó, và thay vào chỗ nhánh này chỉ một nút chứa giá trị X. Như vậy các giá trị khoá vẫn chỉ chứa trong các nút lá nhưng các nút lá giờ đây không chỉ nằm trên mức z + 1 mà còn nằm trên những mức khác nữa. Phương pháp này không những tiết kiệm bộ nhớ hơn mà còn làm cho quá trình tìm kiếm nhanh hơn. Giá phải trả cho phương pháp này là thao tác chèn, xoá khá phức tạp. Tên của cấu trúc dữ liệu này là Trie (Trie chứ không phải Tree) tìm kiếm cơ số.

a)
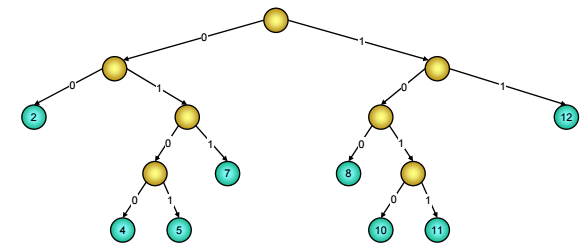
b)
Hình 11: Cây tìm kiếm cơ số a) và Trie tìm kiếm cơ số b)
Tương tự như phương pháp sắp xếp bằng cơ số, phép tìm kiếm bằng cơ số không nhất thiết phải chọn hệ cơ số 2. Ta có thể chọn hệ cơ số lớn hơn để có tốc độ nhanh hơn (kèm theo sự tốn kém bộ nhớ), chỉ lưu ý là cây tìm kiếm số học cũng như cây tìm kiếm cơ số trong trường hợp này không còn là cây nhị phân mà là cây R_phân với R là hệ cơ số được chọn.Trong các phương pháp tìm kiếm bằng cơ số, thực ra còn một phương pháp tinh tuý và thông minh nhất, nó có cấu trúc gần giống như cây nhưng không có nút dư thừa, và quá trình duyệt bit của khoá tìm kiếm không phải từ trái qua phải mà theo thứ tự của các bit kiểm soát lưu tại mỗi nút đi qua. Phương pháp đó có tên gọi là Practical Algorithm To Retrieve Information Coded In Alphanumeric (PATRICIA) do Morrison đề xuất. Tuy nhiên, việc cài đặt phương pháp này khá phức tạp (đặc biệt là thao tác xoá giá trị khoá), ta có thể tham khảo nội dung của nó trong các tài liệu khác.
NHỮNG NHẬN XÉT CUỐI CÙNG
Tìm kiếm thường là công việc nhanh hơn sắp xếp nhưng lại được sử dụng nhiều hơn. Trên đây, ta đã trình bày phép tìm kiếm trong một tập hợp để tìm ra bản ghi mang khoá đúng bằng khoá tìm kiếm. Tuy nhiên, người ta có thể yêu cầu tìm bản ghi mang khoá lớn hơn hay nhỏ hơn khoá tìm kiếm, tìm bản ghi mang khoá nhỏ nhất mà lớn hơn khoá tìm kiếm, tìm bản ghi mang khoá lớn nhất mà nhỏ hơn khoá tìm kiếm v.v… Để cài đặt những thuật toán nêu trên cho những trường hợp này cần có một sự mềm dẻo nhất định.
Cũng tương tự như sắp xếp, ta không nên đánh giá giải thuật tìm kiếm này tốt hơn giải thuật tìm kiếm khác. Sử dụng thuật toán tìm kiếm phù hợp với từng yêu cầu cụ thể là kỹ năng của người lập trình, việc cài đặt cây nhị phân tìm kiếm hay cây tìm kiếm cơ số chỉ để tìm kiếm trên vài chục bản ghi chỉ khẳng định được một điều rõ ràng: không biết thế nào là giải thuật và lập trình.
Bài tập
Bài 1
Hãy thử viết một chương trình SearchDemo tương tự như chương trình SortDemo trong bài trước. Đồng thời viết thêm vào chương trình SortDemo ở bài trước thủ tục TreeSort và đánh giá tốc độ thực của nó.
Bài 2
Tìm hiểu các phương pháp tìm kiếm ngoài, cấu trúc của các B_cây
Bài 3
Tìm hiểu các phương pháp tìm kiếm chuỗi, thuật toán BRUTE-FORCE, thuật toán KNUTH- MORRIS-PRATT, thuật toán BOYER-MOORE và thuật toán RABIN-KARP.
Tuy gọi là chuyên đề về "Cấu trúc dữ liệu và giải thuật" nhưng thực ra, ta mới chỉ tìm hiểu qua về hai dạng cấu trúc dữ liệu hay gặp là danh sách và cây, cùng với một số thuật toán mà "đâu cũng phải có" là tìm kiếm và sắp xếp. Không một tài liệu nào có thể đề cập tới mọi cấu trúc dữ liệu và giải thuật bởi chúng quá phong phú và liên tục được bổ sung. Những cấu trúc dữ liệu và giải thuật không "phổ thông" lắm như lý thuyết đồ thị, hình học, v.v… sẽ được tách ra và sẽ được nói kỹ hơn trong một chuyên đề khác.
Việc đi sâu nghiên cứu những cấu trúc dữ liệu và giải thuật, dù chỉ là một phần nhỏ hẹp cũng nảy sinh rất nhiều vấn đề hay và khó, như các vấn đề lý thuyết về độ phức tạp tính toán, vấn đề NP_đầy đủ v.v… Đó là công việc của những nhà khoa học máy tính. Nhưng trước khi trở thành một nhà khoa học máy tính thì điều kiện cần là phải biết lập trình. Vậy nên khi tìm hiểu bất cứ cấu trúc dữ liệu hay giải thuật nào, nhất thiết ta phải cố gắng cài đặt bằng được. Mọi ý tưởng hay sẽ chỉ là bỏ đi nếu như không biến thành hiệu quả, thực tế là như vậy.