Giải thuật và lập trình - C: I. Các thuật ngữ cơ bản trên cây
Giải phóng thời gian, khai phóng năng lực
I. CÁC THUẬT NGỮ CƠ BẢN TRÊN CÂY
Cây là một tập hợp các phần tử gọi là nút (nodes) trong đó có một nút được phân biệt gọi là nút gốc (root). Trên tập hợp các nút này có một quan hệ, gọi là mối quan hệ cha - con (parenthood), để xác định hệ thống cấu trúc trên các nút. Mỗi nút, trừ nút gốc, có duy nhất một nút cha. Một nút có thể có nhiều nút con hoặc không có nút con nào. Mỗi nút biểu diễn một phần tử trong tập hợp đang xét và nó có thể có một kiểu nào đó bất kỳ, thường ta biểu diễn nút bằng một kí tự, một chuỗi hoặc một số ghi trong vòng tròn. Mối quan hệ cha con được biểu diễn theo qui ước nút cha ở dòng trên nút con ở dòng dưới và được nối bởi một đoạn thẳng. Một cách hình thức ta có thể định nghĩa cây một cách đệ qui như sau:
1. Định nghĩa
- Một nút đơn độc là một cây. Nút này cũng chính là nút gốc của cây.
- Giả sử ta có n là một nút đơn độc và k cây T1,.., Tk với các nút gốc tương ứng là n1,.., nk thì có thể xây dựng một cây mới bằng cách cho nút n là cha của các nút n1,.., nk. Cây mới này có nút gốc là nút n và các cây T1,.., Tk được gọi là các cây con. Tập rỗng cũng được coi là một cây và gọi là cây rỗng kí hiệu .
Ví dụ: xét mục lục của một quyển sách. Mục lục này có thể xem là một cây
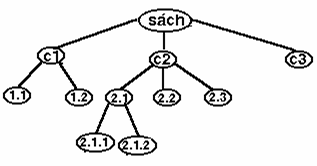
Hình III.1 - Cây mục lục một quyển sách
Nút gốc là sách, nó có ba cây con có gốc là C1, C2, C3. Cây con thứ 3 có gốc C3 là một nút đơn độc trong khi đó hai cây con kia (gốc C1 và C2) có các nút con.
Nếu n1,.., nk là một chuỗi các nút trên cây sao cho ni là nút cha của nút ni+1, với i=1..k-1, thì chuỗi này gọi là một đường đi trên cây (hay ngắn gọn là đường đi ) từ n1 đến nk. Độ dài đường đi được định nghĩa bằng số nút trên đường đi trừ 1. Như vậy độ dài đường đi từ một nút đến chính nó bằng không.
Nếu có đường đi từ nút a đến nút b thì ta nói a là tiền bối (ancestor) của b, còn b gọi là hậu duệ (descendant) của nút a. Rõ ràng một nút vừa là tiền bối vừa là hậu duệ của chính nó. Tiền bối hoặc hậu duệ của một nút khác với chính nó gọi là tiền bối hoặc hậu duệ thực sự. Trên cây nút gốc không có tiền bối thực sự. Một nút không có hậu duệ thực sự gọi là nút lá (leaf). Nút không phải là lá ta còn gọi là nút trung gian (interior). Cây con của một cây là một nút cùng với tất cả các hậu duệ của nó.
Chiều cao của một nút là độ dài đường đi lớn nhất từ nút đó tới lá. Chiều cao của cây là chiều cao của nút gốc. Độ sâu của một nút là độ dài đường đi từ nút gốc đến nút đó. Các nút có cùng một độ sâu i ta gọi là các nút có cùng một mức i. Theo định nghĩa này thì nút gốc ở mức 0, các nút con của nút gốc ở mức 1.
Ví dụ: đối với cây trong hình III.1 ta có nút C2 có chiều cao 2. Cây có chiều cao 3. nút C3 có chiều cao 0. Nút 2.1 có độ sâu 2. Các nút C1,C2,C3 cùng mức 1.
2. Thứ tự các nút trong cây
Nếu ta phân biệt thứ tự các nút con của cùng một nút thì cây gọi là cây có thứ tự, thứ tự qui ước từ trái sang phải. Như vậy, nếu kể thứ tự thì hai cây sau là hai cây khác nhau:
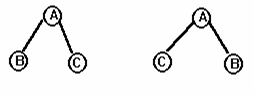
Hình III.2: Hai cây có thứ tự khác nhau
Trong trường hợp ta không phân biệt rõ ràng thứ tự các nút thì ta gọi là cây không có thứ tự. Các nút con cùng một nút cha gọi là các nút anh em ruột (siblings). Quan hệ "trái sang phải" của các anh em ruột có thể mở rộng cho hai nút bất kỳ theo qui tắc: nếu a, b là hai anh em ruột và a bên trái b thì các hậu duệ của a là "bên trái" mọi hậu duệ của b.
3. Các thứ tự duyệt cây quan trọng
Duyệt cây là một qui tắc cho phép đi qua lần lượt tất cả các nút của cây mỗi nút đúng một lần, danh sách liệt kê các nút (tên nút hoặc giá trị chứa bên trong nút) theo thứ tự đi qua gọi là danh sách duyệt cây. Có ba cách duyệt cây quan trọng: Duyệt tiền tự (preorder), duyệt trung tự (inorder), duyệt hậu tự (posorder). Có thể định nghĩa các phép duyệt cây tổng quát (xem hình III.3) một cách đệ qui như sau:

Hình III.3
► Cây rỗng thì danh sách duyệt cây là rỗng và nó được coi là biểu thức duyệt tiền tự, trung tự, hậu tự của cây.
► Cây chỉ có một nút thì danh sách duyệt cây gồm chỉ một nút đó và nó được coi là biểu thức duyệt tiền tự, trung tự, hậu tự của cây.
► Ngược lại: giả sử cây T có nút gốc là n và có các cây con là T1,..,Tn thì:
# Biểu thức duyệt tiền tự của cây T là liệt kê nút n kế tiếp là biểu thức duyệt tiền tự của các cây T1, T2, .., Tn theo thứ tự đó.
# Biểu thức duyệt trung tự của cây T là biểu thức duyệt trung tự của cây T1 kế tiếp là nút n rồi đến biểu thức duyệt trung tự của các cây T2,.., Tn theo thứ tự đó.
# Biểu thức duyệt hậu tự của cây T là biểu thức duyệt hậu tự của các cây T1,T2,.., Tn theo thứ tự đó rồi đến nút n.
Ví dụ cho cây như trong hình III.4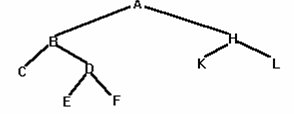
Hình III.4 Cây nhị phân
Biểu thức duyệt tiền tự: A B C D E F H K L
trung tự: C B E D F A K H L
hậu tự: C E F D B K L H A
4. Cây có nhãn và cây biểu thức
Ta thường lưu trữ kết hợp một nhãn (label) hoặc còn gọi là một giá trị (value) với một nút của cây. Như vậy nhãn của một nút không phải là tên nút mà là giá trị được lưu giữ tại nút đó. Nhãn của một nút đôi khi còn được gọi là khóa của nút, tuy nhiên hai khái niệm này là không đồng nhất. Nhãn là giá trị hay nội dung lưu trữ tại nút, còn khoá của nút có thể chỉ là một phần của nội dung lưu trữ này. Chẳng hạn, mỗi nút cây chứa một record về thông tin của sinh viên (mã SV, họ tên, ngày sinh, địa chỉ,...) thì khoá có thể là mã SV hoặc họ tên hoặc ngày sinh tuỳ theo giá trị nào ta đang quan tâm đến trong giải thuật.
Ví dụ: Cây biểu diễn biểu thức (a+b)*(a-c) như trong hình III.5.
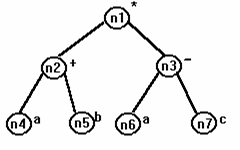
Hình III.5: Cây biểu diễn biểu thức (a+b)*(a-c)
► Ở đây n1, n2,.., n7 là các tên nút và *,+,-,a,b,c là các nhãn.
► Qui tắc biểu diễn một biểu thức toán học trên cây như sau:
► Mỗi nút lá có nhãn biểu diễn cho một toán hạng.
► Mỗi nút trung gian biểu diễn một toán tử.
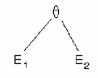
Hình III.6: Cây biểu diễn biểu thức E1q E2
► Giả sử nút n biểu diễn cho một toán tử hai ngôi q ( chẳng hạn + hoặc * ), nút con bên trái biểu diễn cho biểu thức E1, nút con bên phải biểu diễn cho biểu thức E2 thì nút n biểu diễn biểu thức E1q E2, xem hình III.6. Nếu q là phép toán một ngôi thì nút chứa phép toán q chỉ có một nút con, nút con này biểu diễn cho toán hạng của q.
► Khi chúng ta duyệt một cây biểu diễn một biểu thức toán học và liệt kê nhãn của các nút theo thứ tự duyệt thì ta có:
- Biểu thức dạng tiền tố (prefix) tương ứng với phép duyệt tiền tự của cây.
- Biểu thức dạng trung tố (infix) tương ứng với phép duyệt trung tự của cây.
- Biểu thức dạng hậu tố (posfix) tương ứng với phép duyệt hậu tự của cây.
Ví dụ: đối với cây trong hình III.5 ta có:
- Biểu thức tiền tố: *+ab-ac
- Biểu thức trung tố: a+b*a-c
- Biểu thức hậu tố: ab+ac-*
Chú ý rằng
► Các biểu thức này không có dấu ngoặc.
► Các phép toán trong biểu thức toán học có thể có tính giao hoán nhưng khi ta biểu diễn biểu thức trên cây thì phải tuân thủ theo biểu thức đã cho. Ví dụ biểu thức a+b, với a,b là hai số nguyên thì rõ ràng a+b=b+a nhưng hai cây biểu diễn cho hai biểu thức này là khác nhau (vì cây có thứ tự).
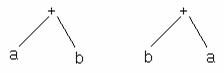
Hình III.7 - Cây cho biểu thức a+b và b+a.
► Chỉ có cây ở phía bên trái của hình III.7 mới đúng là cây biểu diễn cho biểu thức a+b theo qui tắc trên.
► Nếu ta gặp một dãy các phép toán có cùng độ ưu tiên thì ta sẽ kết hợp từ trái sang phải. Ví dụ a+b+c-d = ((a+b)+c)-d.
Giải phóng thời gian, khai phóng năng lực