Lập trình C: Đệ quy (Recursion)
Giải phóng thời gian, khai phóng năng lực
Ngôn ngữ C cho phép hàm gọi đến chính nó, người ta gọi phương pháp này là phương pháp đệ quy hoặc quay lui (xem thêm bài viết Đệ quy và giải thuật đệ quy).
Cú pháp:
* Thường những hàm có kiểu dữ liệu trả về khác kiểu void mới sử dụng được đệ quy (trừ trường hợp ta muốn lặp lại các lệnh tuần tự của hàm thì ta mới dùng đến kiểu void).
* Trong giải thuật này phải có một Điều_kiện_dừng_thỏa để đệ quy kết thúc (dừng quay lui).
* Phép_toán ở đây là một phép toán bất kỳ phù hợp với bài toán của bạn.
* Chương trình sử dụng đệ quy thì dễ hiểu nhưng hao tốn tài nguyên CPU, dẫn đến làm giảm thời gian chạy chương trình đi nhiều nếu số lần đệ quy của hàm lớn.
Ví dụ 1:
Tính tổng các số chia hết cho 5 nằm trong đoạn [0,N] với N được nhập từ bàn phím.
Phân tích: Điều kiện dừng thỏa ở đây ta có thể thấy được ngay là khi giá trị của đối số bằng 0 (nếu ta chạy ngược giảm dần từ N) hoặc bằng N (nếu ta chạy xuôi tăng dần từ 0). Vì chỉ tính tổng các số chia hết cho 5 nên cứ mỗi lần đệ quy thì ta lại giảm (hoặc tăng) giá trị của đối số 5 đơn vị rồi tiến hành cộng dồn.
Chương trình được viết như sau:
#include<stdio.h> long tinhTong(int N) { if(N<=0) //nếu N==0 return 0; //thì dừng đệ quy else //nếu không thì return tinhTong(N-1) + N; //tiếp tục đệ quy } main() { int N; do { //tiến hành nhập N printf("\nMoi nhap N: "); scanf("%d", &N); }while(N<1); //N phải là từ 1 trở lên mới hợp lệ printf("\nTong cac so tu 1 den %d la: %ld", N, tinhTong(N)); //tiến hành đệ quy return 0; }
Kết quả:

Ví dụ 2:
Ta có thể lập trình tính giai thừa theo phương pháp đệ quy, vì n!=1*2*3*…(n-1)*n hay n!=n*(n-1)*(n-2)*…*1 --> Giá trị sau chính là giá trị trước cộng thêm 1 (hoặc là giá trị trước trừ đi 1), giá trị kết thúc =1.
Sau đây là phần demo:
#include <stdio.h> long giaiThua(int n) { if(n==0) //điều kiện dừng thỏa return 1; //vì 0!=1 nên n==0 là vị trí kết thúc của đệ quy return n*giaiThua(n - 1); //kiểu n*(n-1)*(n-2)…*1 } //hoặc: giaiThua(n-1)*n với kiểu 1*2*3*…*n main() { int n; printf("Nhap n: "); scanf("%d", &n); printf("Giai thua cua %d la %ld", n, giaiThua(n)); return 0; }
Ví dụ 3:
In ra n phần tử đầu tiên của dãy Fibonanci (1 1 2 3 5 8 13 21 34 …).
Phân tích: Hai phần tử đầu tiên của dãy là hai phần tử khởi tạo (1 1), bắt đầu từ phần tử thứ ba trở đi sẽ tuân theo quy tắc là phần tử sau bằng tổng của hai phần tử ngay trước nó cộng lại (ví dụ 13=5+8). Công thức: n= (n-1) + (n-2). Như vậy có nghĩa ta sẽ sử dụng được phương pháp đệ quy vì nó tuân theo cú pháp đệ quy.
Chương trình được viết như sau:
#include<stdio.h> int fibo(int n) { if(n==0 || n==1) //nếu là hai phần tử đầu tiên của dãy (điều kiện dừng thỏa) return 1; //thì sẽ có giá trị là 1 return fibo(n-1) + fibo(n-2); //nếu không thì tính giá trị của phần tử đó } main() { int n, i; float; printf("\nNhap so phan tu can xem cua day Fibonacci: "); scanf("%d", &n); printf("\n%d phan tu dau tien cua day la:\n\n", n); for(i=0; i<n; i++) printf("%d ", fibo(i)); return 0; }
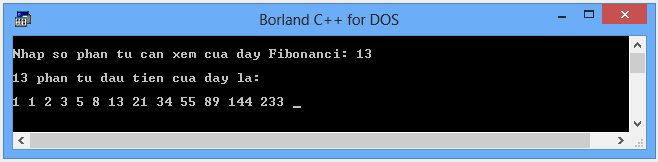
Kết quả:
Giải phóng thời gian, khai phóng năng lực